자료구조: 그래프Graph의 기본적인 이해 (2)

그래프 graph (2) - 기본 개념 이해

그래프의 기본 개념을 설명한 이전 포스팅에 이어서 그래프 정보를 기록하는 두 가지 방법을 소개하고, 탐색 방법 두 가지를 소개합니다.

그래프를 코드로 기록하는 방법

---

그래프를 기록하는 데에는 인접행렬Adjacency Matrix이라는 방법과 인접리스트Adjacency List라는 두 가지 방식이 존재해요.
인접행렬 방식은 행렬 형태로 이차원 배열을 만들어주고 서로 연결되었는지를 기록하고요.
인접리스트 방식은 정점과 연결된 정점의 정보를 링크드리스트로 연결합니다.
두 가지 방식을 예시로 설명하기 위한 구조를 정의해야 할 것 같은데요.
아래와 같은 그래프가 존재한다고 해볼게요.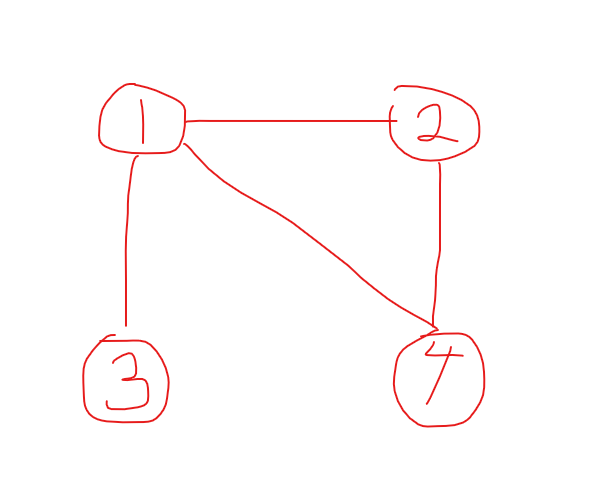

그래프의 예시를 하나 그려봤어요. 이 그림을 가지고 설명해보겠습니다.

인접 행렬 Adjacency Matrix

---

인접행렬 방식의 구체적인 구현은 이렇게 됩니다.
2차원 배열을 만들면 아래 표와 같은 구조가 되겠죠? (배열은 0부터 시작이지만, 쉽고 빠른 이해를 위해서 여기선 생략할게요)

#	1	2	3	4
1
2
3
4

그러면 각 정점의 번호(지금은 1,2,3,4죠)를 인덱스로 보고, 그 사이에 간선이 연결되었는지를 해당 index의 value로 넣는 거예요. 연결되었으면 1, 아니면 0. 이렇게요.
일단 정점 '1'의 간선은 이렇게 존재합니다.

• 1은 1(자기 자신)과 연결되어있지 않다.
• 1은 2와 연결되어있다.
• 1은 3과 연결되어있다.
• 1은 4와 연결되어있다.
  그걸 배열로 표현하면 이렇게 될거에요.

#	1	2	3	4
1	0	1	1	1
2
3
4

아직 헷갈릴 수 있으니까 '2'의 간선 정보까지 기록해볼게요.

• 2는 1과 연결되어있다.
• 2는 2와 연결되어있지 않다.
• 2는 3과 연결되어있지 않다.
• 2는 4와 연결되어있다.

#	1	2	3	4
1	0	1	1	1
2	1	0	0	1
3
4

2에서 3으로 가는 간선이 존재하는데도 연결되어있지 않다고 하죠? 이 행렬의 이름은 '인접'행렬이기 때문에, 바로 옆에 인접해있어야 연결되어있다고 할 수 있기 때문이에요.

전체를 표시하면 이렇게 되겠습니다.

#	1	2	3	4
1	0	1	1	1
2	1	0	0	1
3	1	0	0	0
4	1	1	0	0

지금은 인접 행렬을 표시하는 value를 '연결 되었는지/아닌지'만 고려해서 '1/0'으로 표현했는데요.
간선이 값(가중치)을 가지는 경우에는 해당 가중치를 value로 넣어주기도 하고, 간선의 갯수를 value로 넣어주기도 합니다(사실 가중치와 똑같겠죠?).

인접 리스트 Adjacency List

---

인접리스트는 인접행렬과 마찬가지로 정점과 정점이 바로 인접해 있는지 정보를 기록하는데, 간선 정보를 기록하는 행렬과는 달리 정점 정보를 기록합니다.

먼저 각 정점들을 value로 갖는 배열을 하나 만들고요.

#
1
2
3
4

각 인접 정점들을 링크드리스트 형태로 연결해볼게요. 순서는 중요치 않습니다.
1번 정점을 예로 들면 이렇게 될 거에요.

#
1	2	3	4
2
3
4

2번 정점에 대한 링크드리스트도 만들어볼게요.

#
1	2	3	4
2	1	4
3
4

전부 입력하면 이렇게 되겠네요.

#
1	2	3	4
2	1	4
3	1
4	1	2

인접리스트는 간선이 아닌, 간선에 연결된 두개의 정점의 정보를 기록하는 방식이기 때문에, 총 (간선의 수 * 2)개의 정보를 기록하게 됩니다.

그래프를 탐색하는 방법

---

그럼 이제 그래프를 순회하는 방법에 대해서 알아보겠습니다.
크게 깊이우선탐색DFS, 넓이우선탐색BFS라는 두 가지 방법이 있는데요. DFS는 스택, BFS는 큐로 구현합니다.
어떻게 하는지 자세한 내용은 아래에서 계속 알아볼게요.

깊이 우선 탐색 DFS, Depth-First Search

---

지난 포스트에서 코드로 설명하겠다고 했는데 아직 코드가 한 줄도 안나왔죠?
시간이 부족하고 바빠서 그런 것도 있지만, 이미 설명한 적이 있기 때문이기도 해요.
binary search tree를 설명하면서 말씀드렸던 순회 방식-inorder, preorder, postorder, 이것들이 바로 DFS에 속하는 방식들이에요.
깊이를 기준으로 재귀적으로 탐색하는데, 다음 정점에 방문하면 depth를 내려가며 탐색해요. 끝까지 더 파고들 정점이 없을 때까지 방문한 다음에, 지정한 방식에 따라서 다음 방문할 정점을 방문하게 됩니다.

넓이 우선 탐색 BFS, Breadth-First Search

---

지금까지 계속 BST(binary search tree)를 가지고 예를 들었기 때문에, BFS도 tree를 가지고 예를 들어볼게요.
BSF는 하나의 정점과 연결된 같은 레벨의 정점들, 즉 형제들(siblings)을 동시에 방문하는 방식이에요. 형제들을 모두 방문하고 나면, 그제서야 그 형제들과 연결된 또다른 정점(역시 같은 레벨의)으로 방문합니다.
그렇게 해서 더 방문할 정점이 없을때까지 반복하는 방식을 가지고 넓이우선탐색이라고 말하는 거에요.

마무리

---

당장 써야할 탐색 부분은 코드가 나오지도 않았는데 왜 마무리냐고요?
사실 이번 시간도 맨 위 제목이 '기본 개념 이해'였죠. '활용'이 아니라요. 하하...
분량 조절에 실패해서 탐색 부분은 코드가 등장하지 못한 것입니다. 하핳.. 죄송합니다. 기본 개념만 해도 포스팅 두 번 만으로 다 설명할 수 있는 분량이 당연히 아니었는데, 정신이 좀 없었네요(공부할 게 너무 많아서 그래요!... 공부할게 많아서 물론 좋지만... 정신이 없습니다ㅜㅠ).

다음 포스팅에서는 DFS/BFS를 구현하는 방식을 꼭!꼭!!! 알아보도록 하겠습니다.
감사합니다!!!